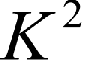Алгоритм Enhanced Self-Organizing Incremental Neural Network (ESOINN)
В данной заметке рассмотрим алгоритм Enhanced Self-Organizing Incremental Neural Network (ESOINN) – предназначенный для классификации входных данных без учителя (неразмеченная выборка). В качестве особенностей алгоритма ESOINN отметим следующие моменты: (i) алгоритм поддерживает обучение в режиме онлайн или lifetime; (ii) алгоритм производит разделение данных с нечёткой границей и выявление основной пространственной (топологической) структуры кластеров; (iii) алгоритм относится к классу самоорганизующихся инкрементных нейронных сетей с адаптивным выбором порогов. При этом алгоритму ESOINN не требуется априорной информации ни о количестве, ни о местоположении определяемых кластеров.
Заметим, что алгоритмы, подобные ESOINN, весьма востребованы в задачах Data Mining, распознавания образов, построения моделей сложных систем и явлений, и находят широкое применение во многих областях: стохастическая финансовая математика; алгоритмический трейдинг; построение скоринговых карт; анализ геологических данных; разработка новых лекарств; анализ медицинских данных; робототехника и т.д.
Алгоритм Enhanced Self-Organizing Incremental Neural Network опубликован в исходной статье: Shen Furao, Tomotaka Ogura, Osamu Hasegawa, An enhanced self-organizing incremental neural network for online unsupervised learning // Neural Networks (2007), 20:(8), pp.893–903. Алгоритм ESOINN является дальнейшим развитием алгоритма SOINN: Self-Organizing Incremental Neural Network, который был опубликован в статье: Shen Furaoa, Osamu Hasegawa, An incremental network for on-line unsupervised classification and topology learning // Neural Networks (2006), 19:(1), pp.90–106.
Сеть ESOINN, в отличии от SOINN, является однослойной, и снимает некоторые ограничения предшественницы, в частности проблему автоматического останова обучения первого слоя, а также является более устойчивой и избирательной при разделении перекрывающихся кластеров. При этом, как показано в исходных статьях, сеть SOINN, в свою очередь, лучше и устойчивее разделяет перекрывающиеся кластеры нежели сеть GNG (growing neural gas).
К сожалению, детальной и корректной информации об алгоритме Enhanced Self-Organizing Incremental Neural Network доступно очень мало (тем более на русском языке), а алгоритм заслуживает внимания. Ко всему прочему, в оригинальной статье местами весьма запутанное изложение, которое существенно усложняет понимание логики алгоритма ESOINN. Поэтому мы и решили поделиться с читателями некоторыми нашими результатами по реализации и тестовым испытаниям алгоритма ESOINN. Пусть это будет нашим скромным подарком к прошедшему 13 сентября 2013 года Дню Программиста.
Отметим заранее, что структура и основные конструкции алгоритма обучения сети ESOINN представлены в псевдокоде, в терминах языка Wolfram Mathematica.
Базовые переменные:
InputSet – массив входных образов;
numImage – индекс входного образа;
Aset – список, содержащий набор узлов;
a1 – индекс первого узла победителя в списке Aset;
a2 – индекс второго узла победителя в списке Aset;
a1pos – позиция первого узла победителя в списке Aset;
a2pos – позиция второго узла победителя в списке Aset;
Tresa1 – порог подобия первого узла победителя;
Tresa2 – порог подобия второго узла победителя;
s – список значений параметра s для узлов, содержащихся в списке Aset;
h – список значений функции плотности для узлов, содержащихся в списке Aset;
M – список значений локальных сигналов для узлов, содержащихся в списке Aset;
SubClassNode – список меток подклассов для узлов, содержащихся в списке Aset;
Cset – список рёбер в формате UndirectedEdge[i, j];
AgeEdge – возраст рёбер, содержащихся в списке Cset.
Управляющие параметры алгоритма ESOINN:
AgeMax – предельный допустимый возраст рёбер, содержащихся в списке Cset.
lambda – количество исходных образов подающихся на вход сети в пределах одного периода обучения.
c1 – константа определяющая порог отнесения узла к шумовому, при наличии у него одного смежного узла (прямого топологического соседа).
c2 – константа определяющая порог отнесения узла к шумовому, при наличии у него двух смежных узлов (прямых топологических соседей).
Непосредственно алгоритм обучения сети ESOINN:
1. Инициализируем исходный набор узлов Аset и другие переменные:
Aset = {{1, InputSet[[1]]}, {2, InputSet[[2]]}};
s = {0, 0};
h = {0, 0};
M = {0, 0};
SubClassNode = {0, 0};
numImage = 3;
Cset = {};
AgeEdge = {};
2. Подаём на вход сети новый образ входных данных:
xi = InputSet[[numImage++]];
3.1. Ищем узлы победители: a1 – первый и a2 – второй.
3.2. Рассчитываем пороги подобия Tresa1 и Tresa2.
3.3. Если дистанция между xi и a1 или a2 больше порогов подобия Tresa1 или Tresa1, соответственно, то добавляем образ xi к списку Aset, и переходим к шагу 2.
4. Увеличиваем возраст всех рёбер инцидентных узлу a1 на 1.
5. Вставляем ребро между узлами a1 и a2.
6. Пересчитываем значение функции плотности h[[a1pos]] для узла победителя.
7. Увеличиваем локальный сигнал для узла победителя, M[[a1pos]]++.
8. Изменяем веса узла победителя и узлов смежных с ним (его прямых топологических соседей).
9. Ищем в списке Cset рёбра, возраст которых превосходит предустановленную константу AgeMax и удаляем их.
10.1. Если Mod[numImage, lambda] != 0 переходим к шагу 2.
10.2. Из списка Aset удаляем узлы, классифицированные как шумовые.
10.3. Переопределяем SubClassNode[[i]], для каждого узла из списка Aset.
11. Если обучение завершилось, формируем выходные данные, иначе переходим к шагу 2.
Ниже приведены основные формулы и конструкции, использованные в приведённом выше алгоритме обучения сети ESOINN.
3.1. Поиск первого и второго узлов победителей: \begin{aligned} a1 = \arg \min_{i\in A}\|\xi - \mathbf{W}_i\|,\quad a2 = \arg \min_{i\in A\backslash\{a1\}}\|\xi - \mathbf{W}_i\|, \end{aligned} где: \(A\) – множество всех узлов из списка Aset; \(\xi\) – входной образ; \(\mathbf{W}_i\) – вектор весов \(i\)-го узла.
3.2. Пороги подобия \(Tres_{a1}\) или \(Tres_{a2}\), соответственно, вычисляются по формулам: \begin{aligned} Tres_{i} = \max \| \mathbf{W}_i-\mathbf{W}_j \|, \quad j\in A^N_i, \end{aligned} где \(A^N_i\) – множество узлов из списка Aset, являющихся смежными (прямыми, топологическими соседями) для узла \(i\). Если узел \(i\) не имеет смежных, тогда пороги рассчитываются по формуле: \begin{aligned} Tres_{i} = \min \| \mathbf{W}_i-\mathbf{W}_j \|, \quad j\in A\backslash\{i\}. \end{aligned}
5. Алгоритм вставки ребра между узлами a1 и a2 (он достаточно нетривиальный, и существенно отличается от такового в сети SOINN):
1) если узлы a1 или a2 не имеют меток принадлежности к тому или иному подклассу (т.е. считаются новыми, метка подкласса установлена в 0), и ребро не существует, то ребро создаётся и возраст этого ребра устанавливается в 0, если же ребро существует, то его возраст устанавливается в 0.
2) если узлы a1 и a2 принадлежат одному подклассу, и ребро не существует, то ребро создаётся и возраст этого ребра устанавливается в 0, если же ребро существует, то его возраст устанавливается в 0.
3) если узлы a1 и a2 принадлежат различным подклассам, то вычисляются параметры:
\begin{aligned}
\hat{h}_{a1} = \max h_i,\quad
\hat{h}_{a2} = \max h_j,\quad
\bar{h}_{a1} = \operatorname{mean} h_i,\quad
\bar{h}_{a2} = \operatorname{mean} h_j,\quad
i\in A_{a1},\quad
j\in A_{a2},
\end{aligned}
здесь \(A_{a\circ}\) – множество всех узлов из списка Aset, относящихся к компоненте связности узла победителя: первого, либо второго. Затем определяется нормировочный множитель:
\begin{aligned}
\alpha_{\circ} = \begin{cases}
0 & 2\,\bar{h}_{\circ} \geqslant \hat{h}_{\circ},\\
1/2 & 3\,\bar{h}_{\circ} \geqslant \hat{h}_{\circ} > 2\,\bar{h}_{\circ},\\
1 & \hat{h}_{\circ} > 3\,\bar{h}_{\circ}.
\end{cases}.
\end{aligned}
Далее производится сравнение:
\begin{aligned}
Satisfied = \begin{cases}
True & \min[h_{a1},\,h_{a2}] > (\alpha_{a1}\, \hat{h}_{a1} \vee \alpha_{a2}\, \hat{h}_{a2}),\\
False & \text{иначе}.
\end{cases}.
\end{aligned}
3.1) если \(Satisfied=True\) и ребро не существует, то ребро создаётся и возраст этого ребра устанавливается в 0, если же ребро существует, то его возраст устанавливается в 0.
3.2) если \(Satisfied=False\) и ребро существует, то оно удаляется.
6. Пересчёт функции плотности узла победителя производится по формулам: \begin{aligned} \bar{d}_i = \frac{1}{\lvert A^N_i \rvert}\sum\limits_{j\in A^N_i} \| \mathbf{W}_i-\mathbf{W}_j \|,\quad j\in A^N_i,\quad p_i = \begin{cases} \cfrac{1}{(1+\bar{d}_i)^2} & i=a1,\\ 0 & \text{иначе}. \end{cases}. \end{aligned} Далее в течении всего периода обучения производится накопление величины \(s_i\): \begin{aligned} s_i = \sum\limits^L_{l=1}\sum\limits^\lambda_{k=1} p_i, \end{aligned} и, наконец, рассчитывается усреднённая плотность узла: \begin{aligned} p_i = \frac{s_i}{q}. \end{aligned} Если необходимо, чтобы в режиме обучения lifetime сеть ESOINN «забывала» слишком старые данные, то \(q = L\), где \(L\) – количество периодов обучения, \(L = \lfloor LT/\lambda\rfloor\), \(LT\) – общее количество входных образов, использованных сетью при обучении, на момент вычисления \(p_i\), а \(\lambda\) – количество исходных образов подающихся на вход сети в пределах одного периода обучения. Если необходимо, чтобы сеть «помнила» даже очень старые данные, то \(q = M_i\). Величина \(M_i\) – это общее количество входных образов, для которых узел \(i\) был первым победителем.
8. Изменение весов первого победителя и узлов смежных с ним, производится по формулам: \begin{aligned} \mathbf{W}_{i} = \mathbf{W}_{i} + \epsilon_1(M_{i})\left(\xi - \mathbf{W}_{i}\right), \quad \mathbf{W}_{j} = \mathbf{W}_{j} + \epsilon_2(M_{i})\left(\xi - \mathbf{W}_{j}\right),\quad j\in A^N_i, \end{aligned} здесь: \(i\) – узел первый победитель. Функции \(\epsilon_1(t)\) и \(\epsilon_2(t)\) в первом приближении имеют вид: \begin{aligned} \epsilon_1(t) = \frac{1}{t}, \quad \epsilon_2(t) = \frac{1}{100\,t}. \end{aligned}
10.2. Правило классификации узлов как шумовые. Узел \(i\) – шумовой: \begin{aligned} A^N_i = \varnothing,\quad \lvert A^N_i \rvert = 1 \wedge h_i < \frac{c_1}{\lvert A \rvert} \sum\limits_{j\in A} h_j,\quad \lvert A^N_i \rvert = 2 \wedge h_i < \frac{c_2}{\lvert A \rvert} \sum\limits_{j\in A} h_j. \end{aligned}
10.3. Алгоритм переопределения списка меток подклассов, в первом приближении, ищет компоненты связности в графе и все вершины одной компоненты, помечает идентичным номером. Для новых узлов удобно использовать значение номера 0. Если Вы пишете на Wolfram Mathematica, то для реализации этого алгоритма удобно использовать функцию ConnectedComponents[...].
Таким образом, на выходе алгоритма ESOINN получаем два списка: Aset – индексы и веса (координаты) узлов; Cset – индексы ребёр. Далее, анализируя топологические и метрические характеристики полученного графа, можно решать множество задач Data Mining, так или иначе связанных с классификацией, кластеризацией и распознаванием образов.
Изложенный алгоритм обучения сети ESOINN был реализован нами в системе Wolfram Mathematica. Для демонстрации результатов его работы рассмотрим ниже два тестовых примера.
Тестовые примеры
Первый пример – три кластера точек, сгенерированных следующим образом:
SizeClassSet1 = 200;
sigma1 = 1.5;
Set11 = Thread@{RandomVariate[NormalDistribution[0, sigma1], SizeClassSet1],
RandomVariate[NormalDistribution[5, sigma1], SizeClassSet1]};
Set12 = Thread@{RandomVariate[NormalDistribution[5, sigma1], SizeClassSet1],
RandomVariate[NormalDistribution[0, sigma1], SizeClassSet1]};
Set13 = Thread@{RandomVariate[NormalDistribution[-5, sigma1], SizeClassSet1],
RandomVariate[NormalDistribution[0, sigma1], SizeClassSet1]};
InputSet1 = RandomSample@Join[Set11, Set12, Set13];
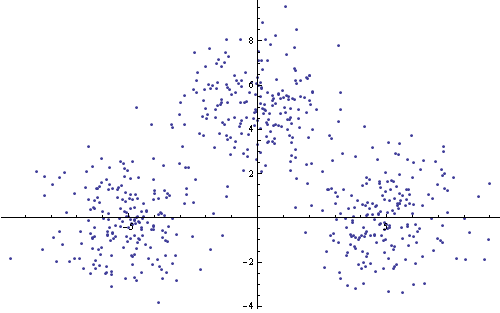
На рисунке ниже приведено изображение тестового множества.
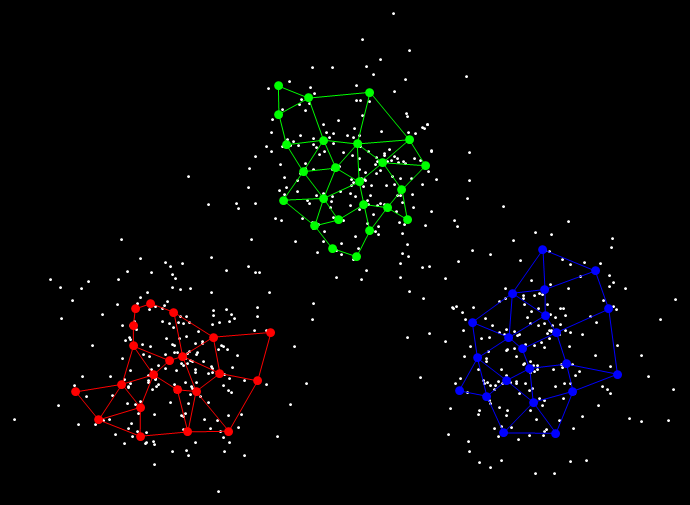
Результат кластеризации показан на следующем рисунке.
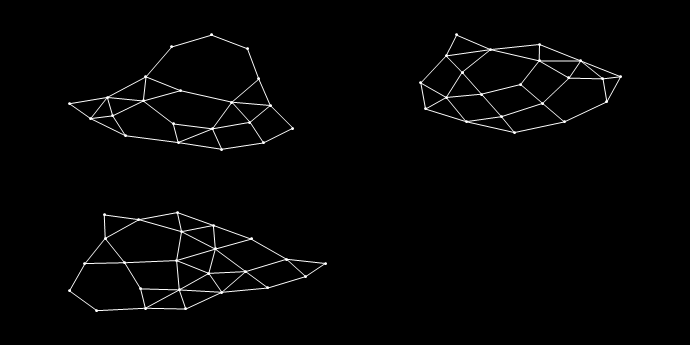
Графы для кластеров приведены на рисунке ниже.
Второй пример – два кластера точек, имеющих нетривиальную форму (топологию). Алгоритм генерации:
SizeClassSet2 = 150;
Set21 = Most@Table[{Cos@alpha, Sin@alpha}, {alpha, 0, 2 \[Pi], 2 \[Pi]/SizeClassSet2}];
Set22 = 2 Most@Table[{Cos@alpha, Sin@alpha}, {alpha, 0, 2 \[Pi], 2 \[Pi]/SizeClassSet2}];
InputSet2 = N@RandomSample@Join[Set21, Set22];
На рисунке ниже приведено изображение тестового множества.
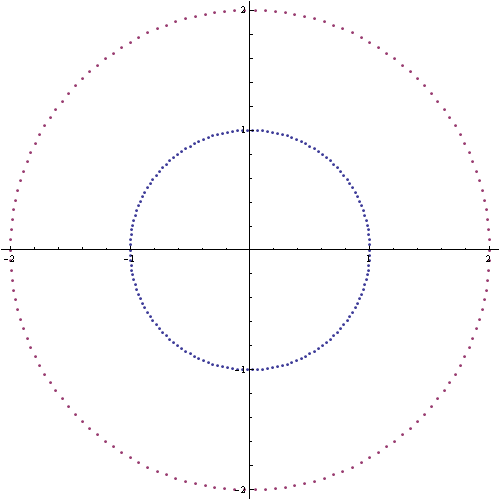
Результат кластеризации показан на следующем рисунке.
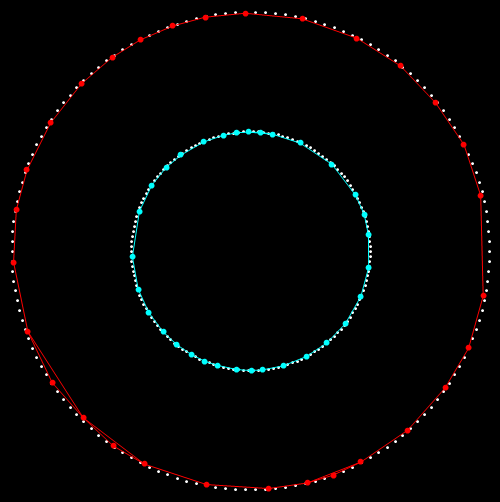
Графы для кластеров приведены на рисунке ниже.
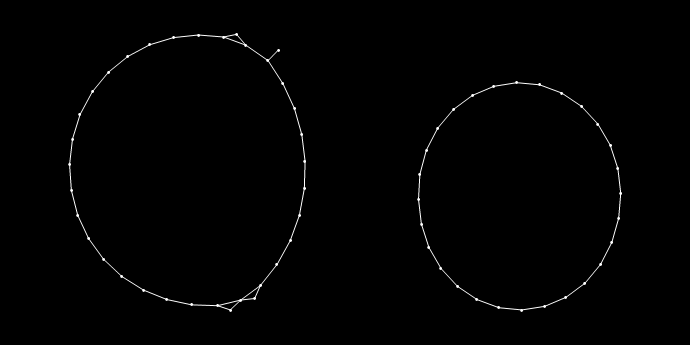
Дополнительные примеры иллюстрирующие работу алгоритма ESOINN Вы также можете найти в оригинальной статье, цитированной выше.
В качестве заключения. Наши исследования алгоритма ESOINN, а также его применение для обработки реальных данных, показало высокую эффективность метода, но при этом требуется аккуратный подбор параметров, управляющих работой алгоритма. Этот процесс весьма желательно автоматизировать, для чего необходимо связать параметры алгоритма и некие дескриптивные характеристики массива входных образов. Решение данной задачи подразумевает интересные и нетривиальные исследования, в аспекте которых у нас уже есть определённое продвижение. Если Вам интересна эта задача – присоединяйтесь к работе!
Данный документ распространяется на условиях лицензии: «Attribution-NonCommercial-NoDerivs» («Атрибуция – Некоммерческое использование – Без производных произведений») CC BY-NC-ND 3.0 Непортированная.
14 сентября 2013 года.
Андрей Макаренко,
группа «Конструктивная Кибернетика».
Обсуждение: contact@rdcn.ru
Ключевые слова: Самоорганизующиеся инкрементные нейронные сети, алгоритм ESOINN, реализация, тестовые примеры.