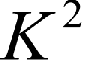Заметки о Deep Learning. Взаимосвязь между нелинейной динамикой и глубокими нейронными сетями. Часть 1.
Научная проблематика, вынесенная в заголовок данной серии заметок о глубоком обучении, на самом деле весьма глубока и широка (интересная игра слов получилась, со смыслом). При этом возможно выделить два основных, в некоем смысле взаимообратных, аспекта отношений нейронных сетей и нелинейной (хаотической) динамики:
Решение отдельных, как правило прикладных, задач нелинейной динамики при помощи нейронных сетей. Для примера см. статью.
Применение методов нелинейной динамики в проектировании, обучении и исследовании глубоких нейронных сетей. Для примера см. статью.
В данной серии заметок о Deep Learning мы скорее будем делать упор на второй аспект взаимоотношений нейронных сетей и нелинейной (хаотической) динамики, как на более фундаментальный. Тем более, что первый (решение задач нелинейной динамики при помощи нейронных сетей) – так или иначе всегда присутствует, когда заходит речь о применении нейронных сетей для задач классификации, предсказания, иной обработки сложно устроенных данных.
Итак, начнём мы с активационной функции ReLU:
\begin{aligned} \mathrm{f}(x) = \max(0,\,x). \end{aligned}График самой функции и её первой производной приведены на рисунке:
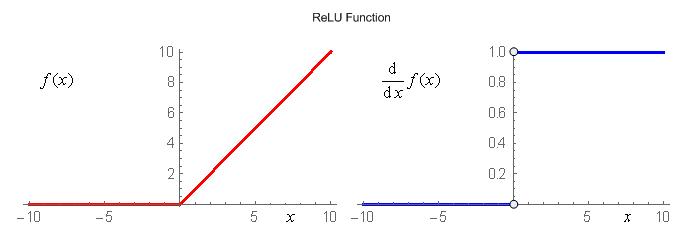
Активационная функция ReLU обладает множеством титулов. В их числе:
ReLU очень быстро вычисляется, в особенности по сравнению с гиперболическим тангенсом, который до определённого времени считался классикой активационных функций.
ReLU сыграла определённую роль в решении краеугольной проблемы целостного (многослойного) обучения глубоких нейросетей – экспоненциального затухания изменений весов в дальних (глубоких) слоях при обучении сети методом обратного распространения ошибки. Положительная роль этой активационной функции проявилась в том, что при \(x>0\) градиент ReLU всюду равен 1, это позволило перейти от послойного unsupervised предобучения сетей к так называемому монолитному обучению сетей на размеченных данных. См. одну из первых статей на эту тему. То обстоятельство, что ReLU недифференцируема в нуле, на самом деле на практике не очень-то и мешает.
ReLU очень популярная активационная функция. Подавляющее большинство современных архитектур глубоких нейронных сетей во внутренних слоях применяют именно её, или её варианты: NoiseReLU, LeakyReLU, PReLU, ThresholdedReLU, SReLU и т.п.
Так, а причём здесь нелинейная динамика?
А нелинейная динамика здесь при том, что на основе функции ReLU возможно сконструировать весьма простое дискретное двумерное отображение:
\begin{aligned} &x_{k+1} = w_{xx}\,x_k+w_{xy}\,y_k+b_x,\\ &y_{k+1} = \max\bigl(0,\,w_{yx}\,x_k+w_{yy}\,y_k+b_y\bigr). \end{aligned}Это отображение (назовём его ReLU_T8a) демонстрирует нетривиальную динамику в ограниченной области фазового пространства. Фазовый портрет аттрактора для начальных условий и параметров:
\begin{aligned} &x_0,\,y_0 \in [0,\,1]\times[0,\,1],\\ &w_{xx}=1,\,w_{xy}=-1,\,b_x=1,\\ &w_{yx}=3/2,\,w_{yy}=1,\,b_y=-1,\\ \end{aligned}приведён на рисунке:
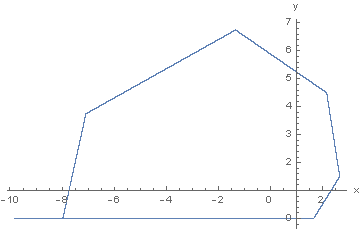
Траектории фазовых переменных отображения ReLU_T8a, входящих в состав указанного аттрактора, имеют следующий вид:
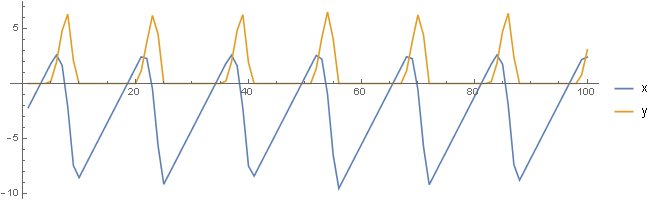
Из рисунка видно, что график фазовой переменной \(x\) – имеет вид «пилообразных» импульсов различной амплитуды, а график фазовой переменной \(y\) – это «игольчатые» импульсы также различной амплитуды.
В следующей части мы продолжим исследовать свойства отображения ReLU_T8а, и раскроем одну из причин синтеза этого своеобразного двумерного дискретного отображения.
Продолжение следует.
07 июня 2016 года.
Андрей Макаренко,
группа «Конструктивная Кибернетика».
Обсуждение: contact@rdcn.ru
Ключевые слова: Глубокие нейронные сети, ReLU, дискретные отображения, аттрактор, хаос.