История освоения Wolfram Mathematica, универсальной и мощной платформы автоматизации интеллектуального труда
Введение
Этот пост, как в общем-то понятно из его названия, про то, как я и мои коллеги осваивали программу Mathematica, и что из этого в итоге вышло. Мотивацией к написанию настоящей заметки послужило три, в общем-то малосвязанных друг с другом, момента.
Во-первых, 02 июля 2013 года, наша научно-исследовательская группа объявила о смене технической политики в области математического моделирования и высокопроизводительных вычислений (подробнее...). И этот пост, в принципе, иллюстрирует и вполне объясняет принятое нами решение, которое при поверхностном взгляде может выглядеть как сильное ограничение.
Во-вторых, 23 июня 2013 года, исполнилось ровно 25 лет постине удивительной программе Wolfram Mathematica. Наше краткое поздравление доступно по ссылке, а настоящую заметку – можно считать его расширенной версией.
В-третьих, в блоге Российского сообщества пользователей системы Mathematica появился минипроект: «Рассказы пользователей Mathematica» (подробнее...). После ознакомления с ним, подумалось, что наша нетривиальная и многоходовая история освоения Wolfram Mathematica, возможно будет интересна читателям и может быть кого-нибудь подвигнет на систематическое изучение и применение этой многогранной и мощной программы.
Данный пост практически не содержит кода и математики и совсем не содержит решения конкретных задач. И причин тому две. Во-первых, заметка и так уже получилась по графомански неприлично объёмной, но как говорится: «из песни слов не выкинешь». Во-вторых, назначение у данного поста иное, нежели технические подробности, он о пути и идеологии.
Здесь необходимо отметить, что все высказывания и мысли об ограничениях/достоинствах тех или иных программ и/или технологий, приведённые в данной заметке ниже – это есть субъективное мнение её автора.
Этапы освоения Wolfram Mathematica
Путь освоения программы Wolfram Mathematica, как можно будет увидеть ниже, у меня был достаточно извилист и в чём-то тернист, и в нём явно прослеживается несколько основных этапов. Эти вехи кратко представлены на интерактивной диаграмме:
Ну а теперь чуть подробнее о каждом из этапов.
2000 г. Версия 4. Первое знакомство.
Да, именно c 4-й версии Wolfram Mathematica началось моё знакомство с этим программным продуктом. Первоначально Mathematica воспринял как систему компьютерной алгебры, но в тоже время и почувствовал мощь и скрытый потенциал программы. В учебной и научной деятельности не применял. Причины этого были разные.
С одной стороны уже достаточно хорошо знал и активно применял для численных вычислений MathCAD. В тех случаях, когда его ресурсов не хватало, расчёты делал в собственных программах, написанных на языке С/C++ с привлечением ряда библиотек численного анализа. С другой стороны, для аналитических расчётов вполне хватало карандаша, ластика и бумаги. Информацию при этом черпал из многочисленных справочников и монографий (преимущественно в печатном виде).
Таким образом, особой потребности в изучении этой сложной и непонятной программы, как тогда казалось (особенно после символьно-графического интерфейса MathCAD) – я не испытывал. Но два слова: Wolfram и Mathematica – в глубинах памяти засели.
2006 г. Версия 5.2. Первая попытка применения.
Прошло 6 лет. За это время мои запросы к вычислительным инструментам выросли, но к версии 5.2 выросла и сама программа Mathematica. Тем не менее, попытка сразу написать на ней объёмный код для численных расчётов оказалась неудачной. Неконтролируемое потребление оперативной памяти (а её на компьютере тогда было существенно меньше 4-х ГБ) и плохая устойчивость кода свели на нет все усилия. Отрицательную роль конечно сыграло и отсутствие навыков программирования на языке Mathematica, а также отсутствие квалифицированной техподдержки в «шаговой» доступности (не встретился нам тогда человек, по знаниям и отзывчивости равный Роману Осипову). Вновь выручил язык С и сторонние библиотеки. А Mathematica была отложена до лучших времён, с мыслью, что Стивен Вольфрам обязательно будет продолжать её улучшать. Но всё чаще стало приходить понимание, что для аналитических математических расчётов карандаша, ластика и бумаги уже хватает не всегда...
2008 г. Версия 6. Редкие случаи применения.
Именно 6-я версия Mathematica стала инструментом, который начал сильно выручать со сложными аналитическими расчётами (и порой не столько сложными, сколько утомительными). Причём выбор пал почему-то не Maple, видимо всё-таки версия 4 Mathematica сделала своё дело... Правда на данном этапе программа использовалась исключительно в режиме последовательного диалога (этакого «умного калькулятора»):
Вычислить производную:
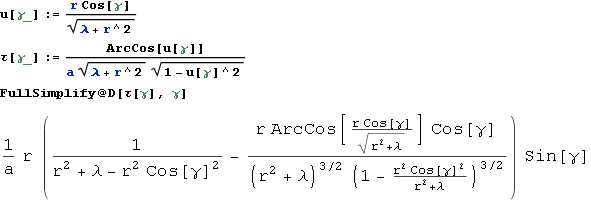
Решить дифференциальное уравнение:
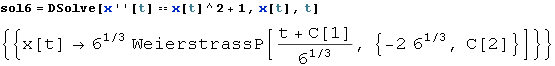
Решить систему алгебраических уравнений:
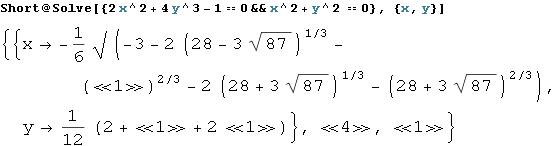
Взять неопределённый интеграл:
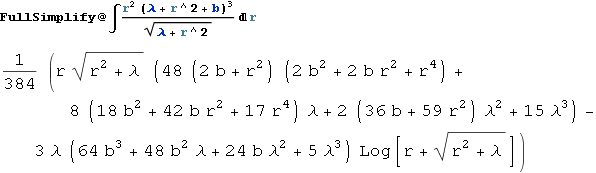
Честно говоря, скорость и лёгкость, с которой Mathematica «щёлкала» приведённые выше примеры – завораживала и притягивала. Тем не менее, использовать программу шире, нежели продвинутый калькулятор, не выходило, видимо не пришло ещё её время. Поэтому простенькие численные расчёты всё также делал на MathCAD, а сложные и ресурсоёмкие – всё также писал на языке С/C++. К тому времени освоил технологии SIMD и OpenMP – программы обрели нитевидный параллелизм на уровне ядер процессора, и жизнь сразу наладилась, но не надолго.
2009 г. Версия 7. Вспомогательный инструмент.
В 2009 году случился переломный момент: возможностей MathCAD, даже для простеньких вычислений, резко стало не хватать, и остро встал вопрос на что мигрировать: Maple, MatLAB, Mathematica, что-то иное. Здесь стоит оговориться, что значит: возможностей стало не хватать. Для производительной и комфортной работы очень хотелось следующих вещей:
Интеграция сильной символьной математики и сильных численных методов в рамках одной программы, одного документа;
Сокращение "зоопарка" программ для сложной визуализации, статистической обработки, анализа графов и т.п. задач;
Возможность гибкой и глубокой настройки внешнего вида графиков и диаграмм для задач когнитивной визуализации;
Прозрачный экспорт математических выражений в нотацию LaTeX для документирования и публикации;
Прозрачный экспорт математических выражений в нотацию языка C при написании программ под HPC кластеры.
Ряд малораспространённых, но интересных программ, а также полуживые Open source решения были отвергнуты сразу. Нужна была масштабируемая платформа с ясным будущим.
Maple был отвергнут из-за своей нестабильности и ограниченности (при решении тех задач, которые нам требовались). Хотя, справедливости ради, стоит отметить, что в то время Maple существенно опережал другие универсальные математические пакеты в вопросах решения дифференциальных уравнений и визуализации их фазовых портретов.
MatLAB проходил по большинству формальных требований, правда символьные вычисления были слабоваты, и интерфейс рабочей области (области вычислений) вызвал противоречивые чувства: неинтуитивный ввод команд, нагромождение окон, и т.п. моменты явно шли ему не в плюс.
Оставалась Mathematica, удовлетворяя и по формальным требованиям, и по интерфейсу рабочей области, который некоторые из моих коллег охарактеризовали как элегантный. На этом муки выбора прекратились. И появилась мотивация. Началось более-менее систематическое изучение синтаксиса и семантики конструкций языка Wolfram Mathematica. В самом начале было трудно, сильно трудно, но здорово выручила книга: [Дьяконов В.П. Mathematica 5/6/7. Полное руководство]. Правда она очень быстро потеряла актуальность, и основное место источника информации занял документационный центр.
Mathematica стала вспомогательным инструментом для численных расчётов – весь необходимый код, ранее созданный в MathCAD начал переноситься в эту среду. Первые программы писались практически исключительно в процедурном стиле (проекция мышления от С/С++ и MathCAD):
QuantityIterations = 1000;
X = RandomReal[{-1, 1}, QuantityIterations];
Y = ConstantArray[0., QuantityIterations];
Do[
Y[[i]] = X[[i]]^2*Sin[\[Pi] Log[X[[i]]]];
,{i, 1, QuantityIterations}];
Ремарка. Кое где в очень старом коде, который приходится использовать повторно, я всё ещё нахожу монстров в виде 5-6-ти вложенных циклов и/или операторов IF THEN ELSE. Естественно, эти места безжалостно рефакторятся, бесплатно давая 2x-13x кратный прирост производительности, придавая коду строгий и лаконичный вид.
Примерно в это же время в моей научной деятельности появились тяжёлые вычислительные задачи, требующие для своей реализации MPI кластеры. Эти задачи конечно программировались на языке C/C++, но макетирование и отладка вычислительных алгоритмов велись на Mathematica.
Большинство аналитических расчётов делалось уже в Mathematica, но всё также в режиме последовательного диалога (на уровне изолированных выражений и операций). При этом отдельные задачи мы стали оформлять в виде цельных ноутбуков, фактически документируя идеи, ход принятия решений, доказательства утверждений, или разработку алгоритмов и процессы вычислений.
Отдельное большое направление применения Mathematica – это когнитивная визуализация результатов расчётов и оформление иллюстраций для публикаций, отчётов, презентаций.
Mathematica стала хорошим помощником. Правда очень сильно не хватало статистических функций и критериев проверки гипотез, функций по вейвлет-анализу, а также ряда специальных возможностей: подгрузки собственных функций и библиотек созданных на языке C/C++; запуск внешних приложений; компилирование функций в С платформу и т. п. фишек.
2010 г. Версия 8. Основной инструмент.
Выход 8-й версии Mathematica ознаменовал собою прорыв. Интерфейс стал стабилен, а сообщения об ошибках ввода и синтаксиса – весьма разнообразными и информативными. Вычислительное ядро прогнозируемо потребляло оперативную память, время исполнения программ было ожидаемо и приемлемо.
Для улучшения наших навыков программирования, и, возможно, спасения своих нервных клеток, наши зарубежные партнёры посоветовали (и дали почитать, за что им большая благодарность) книгу [D.B. Wagner, Power programming with Mathematica], после её прочтения «по диагонали» код немного выправился и преобразился:
QuantityIterations = 1000;
X = RandomReal[{-1, 1}, QuantityIterations];
Y = #^2 Sin[\[Pi] Log@#]&/@X;
После книги D.B. Wagnera и нескольких месяцев упражнений, с десятками «подходов к снаряду», из кода исчезли монстры процедурного стиля, а сам стиль остался в самом минималистичном виде. Т. е. процедурный стиль остался в трёх местах:
где он действительно необходим (в том числе по условию исходной задачи);
где избавление от него занимает неоправданно много времени, а код нужно просто запустить, чтобы опробовать идею;
в весьма запутанных случаях, где у программиста всё ещё не хватает квалификации и навыков функционального программирования и программирования в терминах Rules & Patterns. В борьбе с этим досадным моментом весьма помогает деятельность Леонида Шифрина и хороший форум для сложных и простых вопросов mathematica.stackexchange.com.
Ремарка. Здесь необходимо отметить, что благодаря усилиям сообщества «Российская VK группа Mathematica» и лично Романа Осипова, замечательная книга D.B. Wagnera, стала доступна в электронном виде (см. ссылку).
Переход к функциональному стилю давался нелегко. И основная трудность – это не освоение синтаксиса языка Wolfram, а именно формирование алгоритмического мышления в терминах: Map, Thread, Apply, Rules, Pattern, вместо конструкций for, while, if. Возможно конкретно в этом и заключается ореол таинственности и закрытости Wolfram Mathematica для изучения, при поверхностном взгляде на неё людей, выученных на парадигме языков программирования Fortran, С, Pascal, Basic и им подобных.
Взрывной рост возможностей Wolfram Mathematica, как раз совпал с взрывным ростом наших потребностей: HPC GPGPU CUDA, Data Mining, Data Science, Graph Analysis, Image Analysis, Text Analytics, Nonlinear Dynamic, Big Data. Все сильные ограничения 7-й версии, в 8-й были сняты. Фактически, функционал программы синхронизовался с задачами нашей научно-исследовательской группы (вполне возможно, что и наоборот...).
Mathematica стала применяться для достаточно сложных и ресурсоёмких численных расчётов. К программированию на C/C++ обращались только в самых экстремальных случаях, тем более, что наши зарубежные партнёры предоставляли доступ к GridMathematica кластеру. В общем дело пошло, но мы очень быстро вновь упёрлись в ограничение. Точнее неудобство Mathematica, как среды для разработки и отладки объёмного, алгоритмически насыщенного кода. Но выход был найден практически моментально – это продукт Wolfram WorkBench.
А как же аналитика? Практически все аналитические расчёты были переведены на Wolfram Mathematica, причём глубина использования возможностей символьных вычислений этой программы резко возросла:
(i) многоэтапная обработка символьных выражений с ветвлением операций (путей обработки), как в простеньком иллюстративном примере:.

(ii) а также доказательство некоторых утверждений полным перебором вариантов; машинный синтез моделей (формул) по заданным критериям; и решение массы других задач.
20012 г. Версия 9. Главный инструмент.
И вот в конце 2012 года вышла 9-ка. Интеграция с языком R, поддержка цепей Маркова, расширенная поддержка графов – сняла массу ограничений по статистике и по Machine Learning.
Истинная 64-х битная платформа:

позволила формировать и обрабатывать компактные массивы, содержащие свыше 4-х млрд. элементов.
Расширенный набор Web Operations обеспечивал прямой доступ к данным из среды социальных медиа, существенно ускоряя решение задач класса Data Science.
Расширение возможностей по численному решению дифференциальных уравнений и визуализации их аттракторов, свело на нет воспоминания о возможностях Maple в этой сфере.
Поддержка Image3D и расширенный функционал для работы с изображениями – это просто находка для наших исследований в области приложения Data Mining к биомедицинским проблемам.
Система Wolfram Mathematica 9 – стала нашим главным инструментом решения практически всех без исключения научных задач, как прикладных, так и фундаментальных. Объём .m кода создаваемого в Wolfram WorkBench стал стремительно расти.
Заключение
Итак, я надеюсь, что данный пост позволил читателю получить достаточно цельное представление о том, какими шагами мы двигались на этапе освоения постине удивительной программы Wolfram Mathematica. Кроме того, я также надеюсь, что из данного поста стали понятны причины практически «монопольной» ориентации нашей исследовательской группы на эту универсальную и мощную платформу автоматизации интеллектуального труда.
В качестве небольшого отступления. Мотивация к постоянному изучению Wolfram Mathematica – это эволюция, причём как задач, так и самой программы. Синергия этого процесса порождает знание.
Здесь уместна аналогия. Как известно из истории, первые ЭВМ программировались в машинных кодах, что было достаточно сложной и трудоёмкой задачей. Сильный, качественный прорыв произошёл благодаря разработке первого высокоуровневого языка программирования Фортран в 1954-57 гг. С этого момента взаимодействие человека и компьютера вышло на существенно иной уровень. Возможно сейчас мы наблюдаем следующий виток спирали, в связи с созданием и развитием языка Wolfram.
Скачать данную заметку в формате Wolfram CDF:
![]() HistoryOfMasteringWM.cdf
HistoryOfMasteringWM.cdf
Данный документ распространяется на условиях лицензии: «Attribution-NonCommercial-NoDerivs» («Атрибуция – Некоммерческое использование – Без производных произведений») CC BY-NC-ND 3.0 Непортированная.
13 июля 2013 года.
Андрей Макаренко,
группа «Конструктивная Кибернетика».
Обсуждение: contact@rdcn.ru
Ключевые слова: Wolfram Mathematica, история освоения.