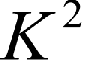Рекурсивный тангенциально-угловой оператор
Проект посвящён исследованию свойств рекурсивного тангенциально-углового оператора: \begin{aligned} \mathrm{TG^a}_k =\operatorname{tg} \prod\limits_{i = 1}^k {\operatorname{arctg}\left[ {{{\left({{c_s}}\right)}_i}\frac{\mathrm{d}}{{\mathrm{d}t}}}\right]}, \end{aligned} а также вопросам его конструктивного применения для анализа структуры динамических процессов и систем. Оператор \(\mathrm{TG^a}_k\) действуя на функцию \({\mathbf{s}}(t)\) порождает систему угловых функций: \begin{aligned} {\vec \alpha}'(t) = \mathrm{TG^a}_1\,{\mathbf{s}}(t),\quad {\vec \varphi_0}'(t) = \mathrm{TG^a}_2\,{\mathbf{s}}(t),\quad {\vec \varphi_i}'(t) = \mathrm{TG^a}_{i+2}\,{\mathbf{s}}(t), \end{aligned} которая фактические описывает форму (структуру геометрии) траектории динамического процесса \(\mathbf{s}(t)\) в пространстве \(\mathrm{S}\times \mathrm{T}\) (для него принимается евклидова метрика). При этом \(\vec{\alpha}'\) – характеризует крутизну графика траектории, а \({{\vec{\varphi }'}_{0}}\) – его кривизну в точке \(t\). Необходимо отметить, что, в отличие от классической кривизны, \({{\vec{\varphi }}'_{0}}\) является динамической кривизной, так как определяется выражением: \begin{aligned} {\vec \varphi _0}'(t) = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \vec \alpha }'}{{\Delta t}} = \frac{\operatorname{d} }{{\operatorname{d} t}}\operatorname{arctg} {\vec \alpha}'(t), \end{aligned} где \(\Delta {\alpha'}^{\,(n)}\) – приращение угла касательной для \(n\)-ой компоненты \(\mathbf{s}(t)\), \(n=\overline{1,\ N}\).
Далее, над системой угловых функций \(\vec{\alpha}'\) и \({{\vec{\varphi }'}_{i}}\), определяются различные конфигурационные, энергетические и информационные величины, которые позволяют охарактеризовать различные свойства динамического процесса \(\mathbf{s}(t)\).
Дополнительно: Публикации по теме проекта.